características y propiedades

números naturales:

Los números naturales son aquellos que permiten contar los elementos de un conjunto. Se trata del primer conjunto de números que fue utilizado por los seres humanos para contar objetos. Uno (1), dos (2), cinco (5) y nueve (9), por ejemplo, son números naturales

Los números naturales pertenecen al conjunto de los números enteros positivos: no tienen decimales, no son fraccionarios y se encuentran a la derecha del cero en la recta real. Son infinitos, ya que incluyen a todos los elementos de una sucesión (1, 2, 3, 4, 5…).

Sin embargo, los números naturales constituyen un conjunto cerrado para las operaciones de suma y multiplicación ya que, al operar con cualquiera de sus elementos, el resultado siempre será un número natural: 5+4=9, 8×4=32. No ocurre lo mismo, en cambio, con la resta (5-12= -7) o con la división (4/3=1,33).

propiedades:

Para cualquier elemento a de A existe b en A tal que a < b

En los números naturales existe el algoritmo de la división. Dados dos números naturales a y b, si b ≠ 0, podemos encontrar otros dos números naturales q y r, denominados cociente y resto respectivamente, tales que:

a = (b × q) + r y r < b

Los números q y r están unívocamente determinados por a y b.

Otras propiedades más complejas de los números naturales, como la distribución de los números primos por ejemplo, son estudiadas por la teoría de números.

Relación de orden

La relación sucesor le da una estructura de orden.10

números enteros:

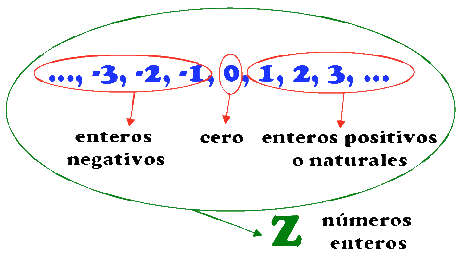
Un número entero es un elemento del conjunto numérico que contiene los números naturales {\displaystyle \mathbb {N} =\{0,1,2,3,\cdots \}} {\displaystyle \mathbb {N} =\{0,1,2,3,\cdots \}}, sus inversos aditivos y el cero.1 Los enteros negativos, como −1 o −3 (se leen «menos uno», «menos tres», etc.), son menores que cero y todos los enteros positivos. Para resaltar la diferencia entre positivos y negativos, se poede escribir un signo «más» delante de los positivos: +1, +5, etc. Y si no se escribe signo al número se asume que es positivo.

En la recta numérica encontramos los números negativos a la izquierda del cero y a su derecha los positivos.

propiedades:

En una recta se ubican a la derecha del cero.

Ej 0, 1, 2, 3, 4, 5, 6, 7...

En ℤ es posible resolver cualquier ecuación de la forma x + a = b

En Z hay una nueva operación ( operación binaria interna) la resta

Tiene la misma coordinalidad que los conjuntos, y de los enteros gausianos y algo mas, lo mismo que el conjunto delos numeros algebraicos.

números primos:

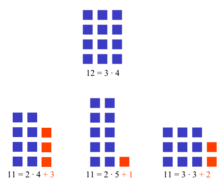
En matemáticas, un número primo es un número natural mayor que 1 que tiene únicamente dos divisores distintos: él mismo y el 1. Por el contrario, los números compuestos son los números naturales que tienen algún divisor natural aparte de sí mismos y del 1 y por lo tanto, pueden factorizarse.

Se puede considerar que los números primos son los «ladrillos» con los que se construye cualquier número natural. Por ejemplo, se puede escribir el número 23.244 como producto de 22·3·13·149, y cualquier otra factorización del 23.244 como producto de números primos será idéntica excepto por el orden de los factores.

La importancia de este teorema es una de las razones para excluir el 1 del conjunto de los números primos. Si se admitiera el 1 como número primo, el enunciado del teorema requeriría aclaraciones adicionales.

A partir de esta unicidad en la factorización en factores primos se desarrollan otros conceptos muy utilizados en matemáticas, tales como el mínimo común múltiplo, el máximo común divisor y la coprimalidad de dos o más números.